نسبت طلایی یکی از مباحث جذاب و در عین حال کمی گیج کننده در هندسۀ ریاضی است که استفاده از آن در طبیعت، هنر، موسقی، معماری و طراحی بسیار رایج میباشد. این نسبت تقریباً برابر با 1.618 بوده و در بیانی ساده از تقسیم یک خط به دو قسمت به دست میآید؛ به گونهای که نسبت قسمت بزرگتر به کوچکتر برابر با نسبت کل خط به قسمت بزرگ تر است.
این قانون به نام های میانگین طلایی، مقطع طلایی، عدد فی (در ریاضیات)، بخش الهی، عدد طلایی، دنبالهی فیبوناچی نیز شناخته میشود. البته دنباله فیبوناچی، خیلی نزدیک به این نسبت است اما دقیقاً یکسان نیست.
نخستین فردی که که فرمول این قانون را کشف کرد، اقلیدس، ریاضیدان یونانی، بود که درباره این موضوع در کتاب خود به نام عناصر توضیح داده است. البته برخی ها معتقد هستند که قدمت این قانون به قبل از این دوره ها باز میگردد.
مستطیل با نسبت طلایی
نسبت طلایی کی از مباحث پیچیده ریاضی است و اگر چندان متوجه آن نشدید، اصلاً نگران نباشید. برای درک بصری این نسبت، مستطیلی را تصور کنید که یک مربع با ضلعی برابر با عرض آن، از داخل مستطیل جدا میشود. حال یک مستطیل کوچک از مستطیل اولیه باقی میماند. نسبت طول به عرض مستطیل ثانویه برابر است با نسبت طول به عرض مستطیل اولیه میباشد.
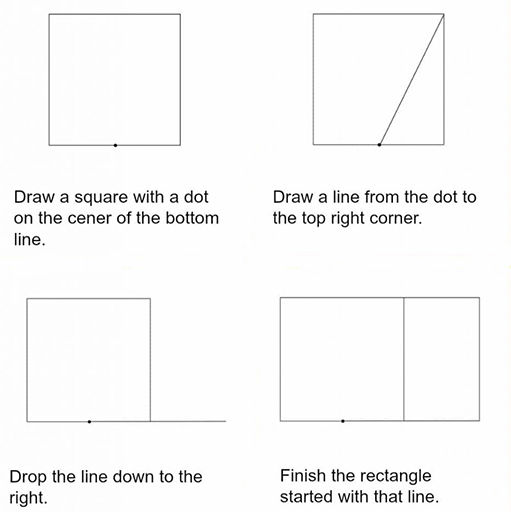
اگر میخواهید بواسطه این نسبت، مسطیلی را رسم کنید، مراحل زیر را به ترتیب طی نمایید:
- مربعی بکشید.
- یک نقطه در نیمهی ضلع پایین رسم کنید.
- خطی از آن نقطه به گوشۀ مقابل آن بکشید.
- خط دیگری را به اندازه طول خطی که رسم شده بود، از نقطۀ نیمهی ضلع پایین مربع به سمت افق (همراستا با ضلع مربع) رسم نمایید.
- هر جا که انتهای خط فرود آید، جایی است که می توانید یک خط رسم کنید و دوباره مستطیل خود را بسازید.
- توجه داشته باشید که مستطیل جدیدی که به تازگی کشیدهاید را می توان به همان نسبت های مستطیل بزرگ جدا کرد. پس می توانید با هر مستطیل بدست آمدۀ کوچک بعدی همین کار را کنید.
- با تقسیم مستطیل جدید به مستطیل های طلایی کوچک،تر و سپس کشیدن یک مارپیچ با استفاده از خطوطی که از یک گوشه به گوشه ی مقابل در هر مربع از مستطیل طلایی میروند، یک قدم جلوتر بروید.
کاربرد تناسب طلایی در دنیا
نسبت طلایی یا عدد فی و یا دنباله فیبوناچی یکی از مباحث هندسی بسیار پر کاربرد در دنیا محسوب میشود. شما نمیتوانید بگویید که انسان صرفاً برای تاثیرگذار کردن بیشتر سازه ها و آثارش از این نسبت استفاده میکند. چراکه این نسبت نه تنها در دست سازهای انسانی، بلکه در طبیعت نیز بسیار از دنباله فیبوناچی استفاده شده است. صدف ناتیلوس (ملوانک)، خطوط ساحلی، گل ها و شکل خود کیهان، مثال های بارزی وجود این مفهوم ریاضی در طبیعت هستند.
علاوه بر آن، تحقیقات و پژوهش های علمی حاکی از آن هستند که ویژگی های خوشایند چهره انسان از این نسبت های الهی به وجود آمده است. بعضی از هنرمندان و ریاضیدانان به نفوذ نسبت طلایی در طبیعت به عنوان نشانهای از ویژگی های زیباشناسی ذاتی آن اشاره میکنند.
تقریباً این طور به نظر میرسد که زیبایی این نسبت درست در ساختار جهان ساخته شده و به همین دلیل انسان ارزش خاصی نسبت به آن قائل است و از آن لذت میبرد. حتی برخی از اندیشمندان معتقد هستند که عدد فی، ماهیت آنچه را که انسان ها «زیبا» به حساب میآورند را تشکیل میدهد.
نسبت طلایی در عکاسی
قانون یک سوم معمولاً به عکاسان مبتدی آموزش داده میشود تا بتوانند با استفاده از این قانون به یک ترکیب بندی نسبتاً مناسبی در عکس هایشان برسند. در این قانون، تصویر موردنظر به 9 فضای برابر تقسیم شده و نقاط کانونی تصویر باید با یک یا چند نقطه در محل تلاقی خطوط، هماهنگ شوند.
نسبت طلایی به عنوان روش دیگری برای تقسیم بندی و ترکیب بندی تصویر، با پیروی از نسبت 1:1.618 استفاده میشود. در این نسبت، خطوط در یک شبکه قرار گرفته اما مانند قانون شبکهی یک سوم، فاصلهی مساوی ندارند.
هر دوی این قانون ها در تلاش هستند که به جای آنکه نقطه کانونی تصویرتان را در یک جا ساکن نگه دارند، چشم بیننده را در اطراف عکس حرکت دهند تا یک ترکیبی جالبتر بوجود آورند. درواقع اینکار باعث بوجود آمدن نوعی تعادل خارج از مرکز میشود که برای ما جالب تر است.
تناسب ابعاد دنباله فیبوناچی، تقریبا با ابعاد 2:3 تصویر دوربین معمولی SLR مطابقت دارد. این نسبت 2:3، سال ها طراحی کلی دوربین های عکاسی را به خود اختصاص داده است؛ چون شباهت نزدیکی با نسبت طلایی دارد.
تجسم دنباله فیبوناچی در عکاسی
در هنگام عکسبرداری، شما موظف هستید که سریع عمل کرده و عکس بگیرید تا سوژه از موقعیت مناسب خود خارج نشود. در نتیجه در این هنگام شما زمان کافی برای محاسبه و اندازهگیری برای دستیابی به نسبت طلایی ندارید تا از آن در ترکیب بندی خود استفاده کنید. اما برای آنکه نتایج عکسبرداریتان به این نسبت نزدیک باشد، کافی است حین عکاسی، صدف ناتیلوس را تصور کنید.
درباره ابعاد دقیق و ایده آل تناسب از دید ریاضی، وسواس نداشته باشید در غیر این صورت شما را بسیار سردرگرم کرده و از مسیر هدف اصلی خارج میکند. تنها کافی است شکلی کلی این هندسه کلاسیک را به ذهن بسپارید. آنگاه به طور ناخوداگاه تصاویری را ثبت میکنید که از این نسبت پیروی کردهاند.
وقتی از محیط بیرون عکاسی میکنید، تلاش نمایید که تناسب طلایی را در محیط اطرافتان ببینید. باید بتوانید امکانی را برای آن تعیین کنید؛ که البته اصلاً آسان نیست. شکل تناسب قرار داده شده روی محیط اطرافتان را تصور کنید. اگر احتمالی را دیدید دیدگاه و زاویه دوربینتان را برای بهتر کردن تاثیر تناسبی تغییر دهید.
